Logicly (3° Parcial)
COMPUERTAS
Las puertas lógicas son componentes fundamentales en la electrónica digital, utilizadas para realizar operaciones lógicas sobre señales binarias. Las tres puertas lógicas más básicas son AND, OR y NOT. A continuación, se describen sus características, funcionamiento y aplicaciones.
Puerta Lógica AND
La puerta lógica AND realiza la operación de multiplicación lógica. Su salida es alta (1) únicamente cuando todas sus entradas son altas (1). Si alguna de las entradas es baja (0), la salida será baja (0).
Función Booleana: S=A⋅B
Aplicaciones: Se utiliza en circuitos donde se requiere que se cumplan todas las condiciones de entrada para activar una salida, como en sistemas de alarmas donde múltiples sensores deben ser activados simultáneamente.
Puerta Lógica OR
La puerta lógica OR realiza la operación de suma lógica. Su salida es alta (1) si al menos una de sus entradas es alta (1). Solo será baja (0) si todas las entradas son bajas funciones.
Función: S=A+B
Aplicaciones: Comúnmente utilizada en sistemas donde se necesita que al menos una condición sea verdadera para activar una acción, como en sistemas de control de temperatura donde un ventilador puede encenderse si cualquiera de los sensores detecta un problema.
Puerta Lógica NOT
La puerta lógica NOT, también conocida como inversor, tiene solo una entrada y su función es invertir el estado lógico de esta. Si la entrada es alta (1), la salida será baja (0), y viceversa.
El álgebra de Boole es una rama de las matemáticas que estudia los valores lógicos y las operaciones entre estos valores. Fue desarrollada por George Boole en el siglo XIX, y es la base del diseño de circuitos digitales y la programación de computadoras. En esta álgebra, los valores solo pueden ser verdadero (1) o falso (0), y se utilizan para representar operaciones lógicas.
Operaciones básicas en el álgebra de Boole
Las principales operaciones que se usan en el álgebra de Boole son:
AND (Y):
- También conocida como conjunción, esta operación devuelve 1 (verdadero) solo si ambas entradas son 1.
- Expresión: A * B
- Tabla de verdad:
A B A AND B 0 0 0 0 1 0 1 0 0 1 1 1
OR (O):
- También conocida como disyunción, esta operación devuelve 1 si al menos una de las entradas es 1.
- Expresión: A + B
- Tabla de verdad:
A B A OR B 0 0 0 0 1 1 1 0 1 1 1 1
NOT (NO):
- También conocida como negación, esta operación invierte el valor de la variable: convierte 1 en 0 y 0 en 1.
- Expresión: A'
- Tabla de verdad:
A NOT A 0 1 1 0
XOR (Exclusivo O):
- Devuelve 1 solo si una de las dos entradas es 1, pero no ambas. Si ambas son iguales, el resultado es 0.
- Expresión: A ⊕ B
- Tabla de verdad:
A B A XOR B 0 0 0 0 1 1 1 0 1 1 1 0
NAND (NO Y):
- Es la negación de la operación AND. Devuelve 0 solo si ambas entradas son 1.
- Expresión: (A * B)'
- Tabla de verdad:
A B A NAND B 0 0 1 0 1 1 1 0 1 1 1 0
NOR (NO O):
- Es la negación de la operación OR. Devuelve 1 solo si ambas entradas son 0.
- Expresión: (A + B)'
- Tabla de verdad:
A B A NOR B 0 0 1 0 1 0 1 0 0 1 1 0
Leyes del álgebra de Boole
Las operaciones de Boole tienen una serie de leyes que facilitan la simplificación de expresiones. Algunas de las más importantes son:
Ley de identidad:
- A * 1 = A
- A + 0 = A
Ley de anulación:
- A * 0 = 0
- A + 1 = 1
Ley de idempotencia:
- A * A = A
- A + A = A
Ley de complementariedad:
- A * A' = 0
- A + A' = 1
Ley de distributividad:
- A * (B + C) = (A * B) + (A * C)
- A + (B * C) = (A + B) * (A + C)
Ley de De Morgan:
- (A * B)' = A' + B'
- (A + B)' = A' * B'
Aplicaciones del álgebra de Boole
El álgebra de Boole se aplica principalmente en:
- Diseño de circuitos digitales: Los circuitos en computadoras, teléfonos y otros dispositivos electrónicos utilizan puertas lógicas (AND, OR, NOT, etc.) para procesar información.
- Sistemas de búsqueda y programación: En informática, se usa para realizar búsquedas en bases de datos, programación de algoritmos y control de flujo en programas.
- Redes y telecomunicaciones: Se utiliza en la implementación de protocolos y en el análisis de señales.
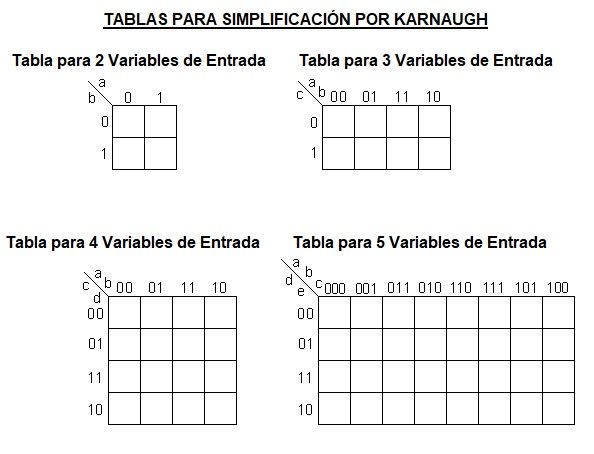
MAPA DE KARNAUGH
Pasos generales para simplificar una función lógica con el método de Karnaugh
Construir el mapa de Karnaugh:
Para una función de 2, 3, 4 o más variables, el mapa será una matriz de celdas donde cada celda representa una combinación de valores de entrada.
Cada celda se llena con un valor correspondiente a la salida de la función lógica en esa combinación de entradas. En el mapa, las celdas pueden contener un valor de 1 o 0, dependiendo del valor de la función en esa combinación de entradas.
Llenar las celdas del mapa:
Si se tiene una tabla de verdad, se usa para colocar los valores 1 en las celdas que corresponden a las salidas verdaderas (1) y 0 en las que corresponden a salidas falsas (0).
Si tienes la expresión booleana en su forma canónica (sumas de productos o productos de sumas), también puedes colocar directamente los 1’s o 0’s en las celdas.
Agrupar los 1’s:
Busca grupos de 1's adyacentes en el mapa de Karnaugh. Los grupos pueden ser de tamaño 1, 2, 4, 8, etc. (tamaño siempre en potencias de 2).
Los grupos deben ser rectangulares o cuadrados, y deben ser lo más grandes posibles para maximizar la simplificación.
Las celdas pueden "envolverse" por los bordes del mapa, es decir, el mapa es cíclico, lo que significa que las celdas del lado derecho se conectan con las del izquierdo, y las celdas de la parte superior con las de la inferior.
Escribir la expresión simplificada:
Para cada grupo de 1’s, se escribe una expresión booleana que representa las variables que permanecen constantes en el grupo.
Se deben eliminar las variables que cambian dentro del grupo. Si una variable tiene tanto 0 como 1 en el grupo, se descarta de la expresión.
Si un grupo cubre varias celdas donde una variable está siempre en 0 o siempre en 1, esta variable se mantiene constante en la expresión.
Escribir la función simplificada:
La expresión booleana final es la suma (OR) de las expresiones correspondientes a cada grupo.
Ejemplo paso a paso
Vamos a simplificar la siguiente función lógica de 3 variables:
F(A, B, C) = Σ(1, 3, 5, 7)
Construcción del mapa de Karnaugh:
El mapa de Karnaugh para 3 variables (A, B, C) tiene 8 celdas, correspondientes a las combinaciones de los valores de A, B, C.
Donde las filas son los valores de A (0 y 1), y las columnas son los valores de BC (00, 01, 11, 10). Los valores 1 en el mapa corresponden a los minitérminos (1, 3, 5, 7).
Llenar el mapa con los valores de la tabla de verdad:
La función F(A, B, C) toma el valor 1 en las posiciones 1, 3, 5 y 7, según la notación Σ(1, 3, 5, 7). Así que colocamos los valores 1 en las celdas correspondientes:
Agrupar los 1's:
Observamos que podemos hacer dos grupos de 1’s:
Un grupo de 4 1's en las posiciones 1, 3, 5 y 7 (en el mapa, estas son las celdas correspondientes a AB=0, BC=01, 11, 10).
Este grupo cubre todas las combinaciones de C (se puede ver que C cambia entre 0 y 1, pero B es constante).
Simplificar la expresión:
Para el grupo de 4 celdas (1, 3, 5, 7): B es constante y C cambia, por lo que el término simplificado es B.
Escribir la función simplificada:
La función simplificada es solo B.
EJERCICIO
Comentarios
Publicar un comentario